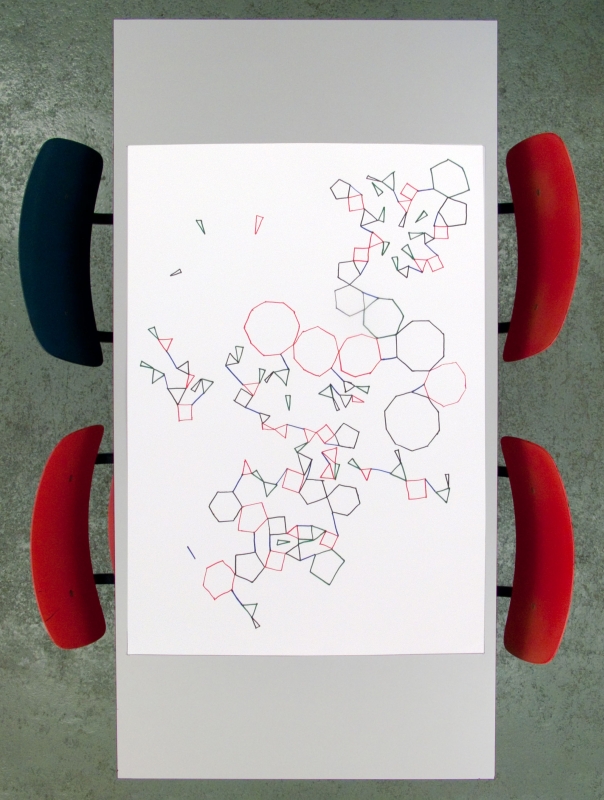
On the 24th of March, 2009,
we drew family trees of flatlanders
Flatland Family Trees
This workshop took its inspiration from the 1884 science fiction novella Flatland: A Romance of Many Dimensions by Edwin A. Abbott.
It describes a two-dimensional world with inhabitants looking like polygons. The hierarchical family structures are described in great detail and determine for the most part the shape of each resident.
The workshop made us create family structures of polygons following the novellas logic with some added rules for positioning the polygons on the paper.
The following types of polygons may be drawn:
name
no. of sides
gender
details
etc...
Rules:
- Participants take turn, drawing one polygon per turn.
- Each participant may only draw polygons of it's own gender.
- Each drawn polygon must have sides with a length of approx. 3 to 4 cm.
- Polygons may not be drawn so that they overlap/intersect.
- A female (line) can be drawn anywhere. She doesn't have any documented parents.
- A male serf (isosceles triangle) can be drawn anywhere. He doesn't have any documented parents.
- All other male polygons can be drawn only when it is connected with one of its corners to a corner of its father (a polygon with one less side than its own, the father of a equilateral triangle is a isosceles triangle) and one of its other corners to a corner of its mother (a line).
- As soon as there occurs a possibility to draw a child, then that child must be drawn. When multiple options are possible, then the participant must choose one.
- Any polygon corner may connect to only one other polygon corner.
Notes:
- Each male may only have one female (his mother) connected to him.
- Each male may only have one one-lower-generation polygon (his father) connected to him.
- Each male can have as many as possible one-higher-generation polygons (his sons) connected to him.
more info on regular polygons:
http://en.wikipedia.org/wiki/Regular_polygon